Una cosa vemos clara: todas las verticales dirigidas al globo solar terminan siendo paralelas y, en consecuencia, todas se confirman como rectas paralelas que jamás podrán intersecarse.
Por ejemplo, las infinitas paralelas o verticales que tracemos desde un segmento o arco de la periferia de una circunferencia incidirían paralelamente en otros arcos de iguales o desiguales longitudes con iguales o desiguales curvaturas- cóncavas y convexas.
Cantor nos enseña que un segmento menor paralelo a otro mayor puede contener la misma cardinalidad de este último. Lo demuestra mediante una secantación de rectas no paralelas.Ver gráfica adjunta.
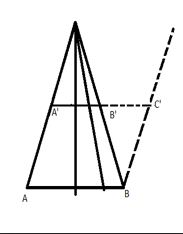
En esa gráfica, Cantor nos afirma que habría tantos puntos geométricos a lo largo del segmento A’B’ como los haya en el segmento AB.
Sin embargo, trazada la paralela BC' a AA’, podemos también afirmar que en los segmentos AB y A’C’ existiría igual número de puntos. En consecuencia, no pueden caber tantos puntos en A’B’ como en A’C’, razón por la cual resulta paradójico que quepan en A’B’ tantos puntos como en AB = A’C’. Esta paradoja podemos llamarla P. de Cantor.
02/09/2015 07:26:21 p.m.

