Dice Franz Hinkelammert en la Reflexión Final del Cap. 5 de su libro "La crítica de las ideologías y de la religión – Volver a Marx trascendiéndolo" (Ed. CLACSO, Buenos Aires, 2021, p. 169):
"Las conclusiones que Marx saca de su crítica de la religión presuponen que la imaginación marxiana del comunismo es algo que se puede realizar con la práctica humana. De eso sigue la muerte de la religión como consecuencia de la realización del comunismo. Sin embargo, si la imaginación del comunismo resulta no realizable, entonces cambian las conclusiones que se derivan de la crítica marxiana de la religión".
Aquí Hinkelammert incurre en el muy conocido sofisma de falsa contraposición, aclarado por la Lógica Clásica desde hace mucho tiempo; así, la forma de razonamiento en cuestión no es una forma válida de razonamiento.
Recordemos que una forma de razonamiento es válida cuando no existe ningún razonamiento con esa forma en el cual es verdadera la conjunción de sus premisas y, sin, embargo, su conclusión es falsa.
Así, una forma de razonamiento es válida cuando la fórmula sentencial a ella asociada es una tautología.
Recordemos: 1) que una fórmula sentencial es una tautología cuando su columna de evaluación está constituida solamente por símbolos de "v", o sea de "verdadero"; 2) que cuando una fórmula sentencial representa una forma de razonamiento, la columna de evaluación de dicha fórmula sentencial está ubicada debajo del operador de implicación (representado aquí en lo que sigue por la segunda flecha "→", de izquierda a derecha, que aparecerá en la fórmula sentencial) que separa a las premisas, por un lado, de la conclusión, por el otro.
Ahora bien, la columna de evaluación de la fórmula sentencial que representa a la forma de razonamiento usada por Hinkelammert, no contiene solo símbolos de "v"; así esa fórmula sentencial no es una tautología; por lo que la forma de razonamiento en cuestión no es lógicamente válida.
La forma usada por Hinkelammert tiene como primera premisa "Si la imaginación marxiana del comunismo se puede realizar por la práctica humana, entonces la religión muere" (que leemos "p implica q").
Su segunda premisa dice: "La imaginación marxiana del comunismo no se puede realizar por la práctica humana" (que leemos "no p").
Y de la conjunción de ambas premisas saca Hinkelammert la conclusión "La religión no muere" (que leemos "no q").
Representamos aquí a la implicación por la flecha "→"; la negación se representa por la tilde, o sea la "viborita"; y la conjunción "y", que une a las dos premisas, se representa por un punto.
En resumen a ese razonamiento se asocia la siguiente forma
Pr. 1 p → q
Pr. 2 ~ p
Ccl. ~ q
En síntesis representamos esa forma de razonamiento como sigue:
p → q . ~ p
-------------------
~ q
(Hemos puesto la conjunción de las premisas arriba de la línea punteada, y la conclusión debajo de ella)
A esa forma de razonamiento corresponde la fórmula sentencial que sigue:
((p → q ). ~p) → (~q)
(En ella ponemos en implicación a la conjunción de las premisas con la conclusión)
Recordemos resumidamente la tabla veritativa de cada uno de los operadores lógicos aquí utilizados: 1) si una sentencia, en este caso "p" o "q", es verdadera, su negación es falsa; 2) para que una conjunción sea falsa basta que una de las sentencias que la forma, en este caso "p" y "q", sea falsa; 3) una implicación es falsa solo cuando su antecedente, o sea la sentencia que va antes de "→" es verdadera, y su consecuente, o sea la sentencia que va después de "→", es falsa.
Ahora bien, al hacer el cálculo, se comprueba que la referida fórmula sentencial no es una tautología (o sea que puede haber por lo menos un razonamiento al cual se puede asociar la forma de razonamiento representada por esa fórmula sentencial, en el que la conjunción de las premisas es verdadera, pero la conclusión es falsa; de donde resulta que la implicación que va de la conjunción de las premisas, por un lado, hacia la conclusión, por otro, es falsa; y, por tanto, en la columna de evaluación de la referida fórmula sentencial aparece por lo menos un símbolo de "f").
Así el hecho de que la fórmula sentencial no sea una tautología determina que la forma de razonamiento que ella representa no es válida.
Sigue abajo el cálculo, resumiendo la indicación de los valores veritativos ("verdadero" o "falso") al mínimo indispensable:
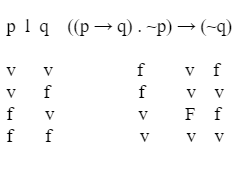 |
En la tercera línea del cálculo se verifica que cuando: 1) "p" es falsa y "q" es verdadera, 2) la conjunción de las premisas es verdadera; ver el símbolo de "v" que en esa línea está debajo del punto que representa la conjunción de las premisas, 3) pero la implicación (la segunda flecha → de izquierda a derecha en la fórmula sentencial) entre la conjunción de las premisas y la conclusión es falsa, lo que hemos señalado con la letra "F" mayúscula; o sea, que en la tercera línea de la columna de evaluación de dicha fórmula sentencial hay un valor que no es "v", sino "f", o sea, es "falso" 4) y ello ocurre porque en esa tercera línea de cálculo el antecedente de la implicación que separa la conjunción de las premisas por un lado, de la conclusión, por el otro, es verdadero, pero su consecuente es falso, en la medida en que la conclusión ("~q") es falsa.
(Reiteramos que el único caso en el que una implicación es falsa es aquel en el que el antecedente de la implicación es verdadero y su consecuente es falso).
Ese símbolo de "falso" (F) en la columna de evaluación indica que la fórmula sentencial en cuestión no es una tautología, y, por lo tanto, la forma de razonamiento que ella representa no es una forma de razonamiento válida.
Apreciemos en lo que sigue un ejemplo de un razonamiento al que podemos asociar la forma de razonamiento en cuestión y donde vemos que hay claramente un error en esa forma de razonar.
La sentencia "p" dice "Este número es un 4".
La sentencia "q" dice "Este número es divisible por 2".
Así la primera premisa (p → q) del razonamiento dice "Si este número es un 4 entonces este número es divisible por dos". Y esa premisa es verdadera.
La segunda premisa (~p) dice "Este número no es un 4". Y esa premisa es verdadera si el número es un 1, o un 5, o un 7; pero también es verdadera si el número en cuestión es un 6, o un 8, o cualquier número par; ahora bien, si el número en cuestión es un 6, un 8 o cualquier número par, la conclusión (~q) que dice "Este número no es divisible por 2", es falsa.
A partir de Aristóteles la Lógica Clásica establece que tenemos derecho a rechazar una forma inválida de razonamiento sin entrar siquiera a considerar el contenido de los enunciados que la componen (en sus premisas y su conclusión). Y eso se puede hacer con el razonamiento empleado por Hinkelammert que aquí hemos analizado.
En lo que concierne a los contenidos abordados por Hinkelammert en el citado fragmento, si bien los mismos requieren un análisis más detenido ( ver, por ejemplo, mis dos textos de 2024 citados en la bibliografía final de estas líneas), resumo lo medular de mi posición/visión como sigue.
La misión nunca acabada de los humanos en su búsqueda de superación de su alienación religiosa (y profana) y por realizarse como individuos universales y cósmicos, al contrario de lo que deduce Hinkelammert, NO valida la religión, sino que confirma el carácter utópico del Ecomunitarismo, en el sentido que Fernando Birri dio a la Utopía diciendo: es algo que cuando caminamos en su dirección diez pasos se aleja diez pasos, y cuando avanzamos cien pasos se aleja cien; pero/y si se nos pregunta para qué sirve la Utopía, responderemos: pues sirve, precisamente, para que no cesemos de caminar.
Así concebimos al Ecomunitarismo como el orden comunitario-ambiental poscapitalista utópico regido en su día a día por las tres normas fundamentales de la Ética y por el principio que reza "De cada un@ según sus capacidades y a cada un@ según sus necesidades, respetando los equilibrios ecológicos y la interculturalidad"; tal orden, no siendo nunca plenamente alcanzable, es, no obstante, una indispensable estrella guía para que nuestra acción cotidiana tenga un rumbo claramente definido, y no vaguemos en círculos o sin dirección fija.
Bibliografía mínima
Ricardo Salas Astraín y José Alberto de la Fuente Arancibia (Orgs.), Introducción al Ecomunitarismo y a la Educación Ambiental. Una lectura chilena de la obra de Sirio López Velasco, Ed. Ariadna, Santiago de Chile, 2021, disponible gratuitamente en https://zenodo.org/record/5745105#.YaZXEdDMI2w ,
en https://dlc.dlib.indiana.edu/dlc/handle/10535/10827
en https://library.oapen.org/handle/20.500.12657/51640
y en https://es.scribd.com/document/561776175/Introduccion-Al-Ecomunitarismo-y-Educacion-Ambiental
Sirio López Velasco, Fundamentos lógico-lingüísticos da ética argumentativa, Ed. Nova Harmonia, São Leopoldo, Brasil, 2003.
--- Ética ecomunitarista, Ed. UASLP, México, 2009; disponible gratuitamente en https://rebelion.org/download/etica-ecomunitarista-etica-para-el-socialismo-del-siglo-xxisirio-lopez-velasco/?wpdmdl=654430&refresh=5ffa00fe3411b1610219774
y en https://www.scribd.com/document/557262193/Etica-ecomunitarista
---, Filosofía ecomunitarista aplicada - Textos breves 2022-2023, (Org. Claudinei A. de Freitas da Silva), Ed. Fi, Cachoeirinha, 2023, disponible gratuitamente en
https://www.editorafi.org/ebook/a042-filosofia-ecomunitarista-aplicada
---- "Cristianocentrismo y autonegación xavante: una crítica desde el Ecomunitarismo" (2024), en https://www.aporrea.org/internacionales/a327833.html
---- "Primeras hipótesis ecomunitaristas sobre la alienación en las religiones indígenas de Abya Yala" (2024), en https://www.aporrea.org/internacionales/a327907.html

